CHAIVERSE: CROWDSOURCING THE LEAP TO TEN TRILLION-PARAMETER AGI
At Chai our mission is to accelerate the advent of AGI through massively distributed collaboration, i.e. crowdsourcing. By appealing to well-known scaling laws [1] we anticipate that achieving this will require a language model with parameters on the order of about 10 trillion. Several companies, such as OpenAI and Anthropic, focus on internal closed-source research, utilising internal datasets and powerful compute clusters to train individual large-parameter models.
At Chai we believe the resources to piece together this large model already exist, but are widely distributed. This is why at Chai we have cultivated a community of developers who currently produce small-size models (7b and 13b parameters) by fine-tuning them on any datasets of their choosing. Once a model is ready, a developer can deploy it via our Chaiverse platform. The model is then served to the Chai App where millions of users can start chatting with it, and provide feedback on the quality thereof.
Since these models are trained by different developers on a wide variety of different datasets, we have discovered that each of them can perform well in some particular “dimension”. For example, some models may excel at “creativity/storytelling”, some might have a very literary way of speaking, some might be “intelligent”, while others still might be “fun”.
MoEs Are Recommender Systems
The challenge, then, is to leverage these wide varieties of models and to serve them in a way that is best aligned with the user’s expectation. This is indeed very similar to the so-called Mixture-of-Experts (MoE) architectures, which consist of several small models (the “experts”). At inference time, one (or even several) expert models are selected to generate the output. The selection is done via an auxiliary gating model, which, based on the input, selects which model to use for inference.
This approach offers multiple advantages:
- Lower training costs: Training small-size models is accessible to a wider range of developers. Indeed, it is well known that training large-parameter LLMs is a prohibitively expensive task, and as a result is inaccessible to most machine learners.
- Lower inference costs: The inference cost of a multitude of small expert models is lower than that of a single large model.
- Higher iteration speed: Small models can be trained and deployed much faster than large ones, allowing for much shorter feedback loops and higher iteration speed.
Usually, MoE models are all trained together along with the gating model on a wide variety of datasets. This is however not the case at Chai: our experts have already been trained by the community, and our goal is to build the gating model. The Chai gating model, which we typically refer to as an LLM-controller is equivalent to a recommender system which takes as input a conversation and has, as output, the recommended expert model to serve.
Connecting Millions of LLMs with Chai LLM-Controller
How should this controller system work at a high level? The usual approach is to write the score of serving a model \( m \) for a given conversation \( C \) as: $$ \operatorname{score}(m \mid \mathcal{C})=\theta_m \cdot x_{\mathcal{C}}, $$
where \( \theta_m \) and \( x_{\mathcal{C}} \) are relatively low-dimensional “feature” vectors obtained by representing the model and conversation state together in some common ambient feature-space. The higher the score, the more aligned the model \( m \) is to the conversation.
These feature vectors can be taken to be the “dimensions” which we discussed in the introduction. To illustrate this, let’s imagine we have at our disposal three dimensions: [role-play, creative, informative]. Then we can consider the following feature vectors, together with the accompanying score: $$\left.\begin{array}{l} \theta_m=[0.1,0.8,0.3] \\ x_{\mathcal{C}}=[0.4,0.3,0.7] \end{array}\right\} \rightarrow \text { score }=0.49$$
The goal of the LLM-controller would then be to optimise this, seeking those models \( m \) with the highest such score. When building such a recommender system, there are three main parts we need to investigate:
- What is the most sensible metric to optimise?
- How do we determine the feature space?
- What does our training dataset look like?
Metrics
Chai’s north-star metric is user-engagement, which we calculate by analysing user screen-time on the Chai app. This metric is typically measured via A/B testing our various models, with the LLM-controller serving a useful role in determining which are the strongest models to serve in such a test.
User-engagement is inherently a noisy metric for measuring the performance of models, as it incorporates other effects, such as ongoing changes to the Chai app’s frontend. In order to better resolve a model’s impact, it is useful to decompose engagement into a series of proxy message-level metrics.
There exist a few such offline metrics which have worked well when training our reward models:
- retry: was the message retried?
- rating: what was the star rating of the message?
- conversation length: how long was the conversation after the message was sent.
For the purpose of the LLM-controller, it is a rather subtle question as to whether these metrics are sufficient, whether there could exist other more useful ones, or even whether a combination of such metrics is better-suited:
$$\mathcal{L}_{\text {loss }}=\alpha_{\text {retry }} \cdot \mathcal{L}_{\text {retry }}+\alpha_{\text {rating }} \cdot \mathcal{L}_{\text {rating }}+\alpha_{\mathrm{CL}} \cdot \mathcal{L}_{\mathrm{CL}},$$where \( \alpha \) are hyperparameters which we can tune.
Features
In order to score a model \( m \)’s suitability for a conversation \( \mathcal{C} \), we must map them to a set of \( k \) numbers: the “feature space”. The conversation being a string, we can tokenise it and use language model to map it to a feature space:
$$\mathcal{C} \xrightarrow{\text { tokenizer }}\left[t_1, \ldots, t_n\right] \xrightarrow{\text { LLM }} x_{\mathcal{C}}$$Of course, the LLM architecture needs to be selected and its parameters determined via training.
The question of how to map a model to a subset of \( k \) features is, however, more complicated:
$$ m \stackrel{?}{\longrightarrow} \theta_m $$At this point, the literature on recommender systems often delineates two approaches to this problem [2] :
- Collaborative-based filtering: In this approach, one considers a finite set of models \( [m_1,\ldots, m_n] \), together with a set of trainable weights \( \theta_{m\,i}\in\mathbb{R}^{n\times k} \) which will be determined through training. This is the approach that several large-scale algorithms take, such as YouTube’s video recommender system [3]. The advantage of this approach is that we remain agnostic on the nature of the \( k \)-dimensional feature space: the model itself is able to learn the embeddings on the fly. The inconvenience is that 1) we lose interpretability of the feature space and, mainly, 2) the model would need to be frequently retrained in order to learn the embeddings for newly introduced expert models: a rather daunting engineering task.
- Content-based filtering: The second approach is to independently model the mapping from expert models to the feature space. One way to accomplish this is to ask another language model (such as GPT4) to score the response of each expert model on a set of (dataset x categories). The great advantage is that each model can be scored on a feature space without the need for retraining. The inconvenience is that we make a conscious, and possibly limiting, decision of what we think the features (or categories) should be.
It is also worth noting that many find success in a hybrid approach, where the model trained in the collaborative approach has its dataset augmented with some fixed additional features via the content-based approach.
Early Experiments: +68% Engagement VS. GPT3.5
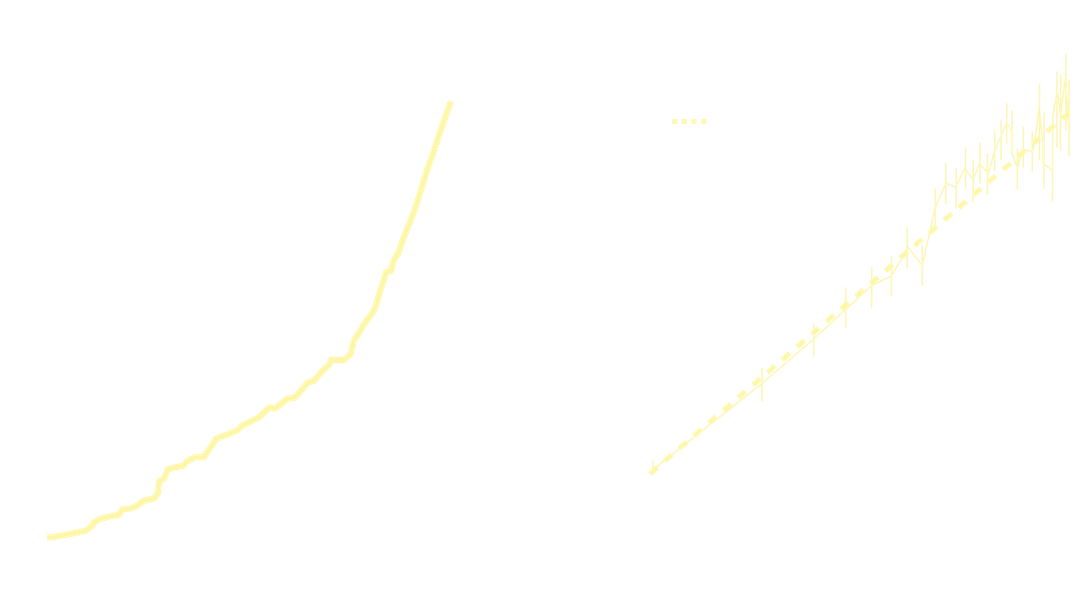
At Chai, the open-source solution is already well underway. Chaiverse, our developer platform, was first launched on April 4th 2023. It provides a space for developers to connect with millions of unique users, take onboard feedback and iterate and improve their models almost immediately. Because of this large influx of creators, the language model powering Chaiverse has already grown to a trillion parameters, with over 1211 unique expert models submitted to the platform, allowing for a level of customised AI interaction as never seen before. The early results were extremely promising. A carefully optimized mixture of 7B models had outperformed OpenAI's GPT-3.5. Over a four-month period, our in-house LLMs had achieved a 20% day-30 engagement improvement, compared with GPT-3.5 models. However, when the top models from the Chaiverse LLM competition were combined, day-30 engagement levels were raised by 40% from the in-house models, marking a 68% total increase from GPT-3.5.